2021.05.24 - [Study/NLP] - [NLP/자연어처리] Seq2Seq(1) - RNN을 이용한 시퀀스 투 시퀀스
[NLP/자연어처리] Seq2Seq(1) - RNN을 이용한 시퀀스 투 시퀀스
이전 RNN, LSTM, GRU에 대한 글을 보려면 아래 참조 2021.05.20 - [Study/NLP] - [NLP/자연어처리] 순환신경망 (Recurrent Neural Network, RNN) [NLP/자연어처리] 순환신경망 (Recurrent Neural Network, RNN) 해..
everywhere-data.tistory.com
2021.05.24 - [Study/NLP] - [NLP/자연어처리] Seq2Seq(2) - 어텐션 매커니즘(Attention Mechanism)
[NLP/자연어처리] Seq2Seq(2) - 어텐션 매커니즘(Attention Mechanism)
2021.05.24 - [Study/NLP] - [NLP/자연어처리] Seq2Seq(1) - RNN을 이용한 시퀀스 투 시퀀스 [NLP/자연어처리] Seq2Seq(1) - RNN을 이용한 시퀀스 투 시퀀스 이전 RNN, LSTM, GRU에 대한 글을 보려면 아래 참조 20..
everywhere-data.tistory.com
트랜스포머를 이해하는데 너무 힘들었다. 과정이 너무 길고 복잡해서인지 하루 종일 따라갔다. 역시 구글은 대단해...
딥러닝을 이용한 자연어 처리 입문 과 강필성 교수님의 강의자료를 바탕으로 포스팅을 작성한다.
1. Transformer
트랜스포머(Transformer)는 2017년 구글이 발표한 논문인 "Attention is all you need"에서 나온 모델로 기존의 seq2seq구조인 인코더-디코더 모양을 따르면서도, 논문의 이름처럼 어텐션(Attention)만으로 구현한 모델이다. Transformer는 RNN cell을 사용하지 않고 어텐션만을 사용하여 seq2seq 모형을 설계하면서 속도와 성능이 모두 우수하다는 장점을 가지고 있다.

트랜스포머는 RNN을 사용하지 않지만 Seq2Seq의 형태를 띄고 있으므로 인코더에서 입력 시퀀스를 입력받고, 디코더에서 출력 시퀀스를 출력하는 인코더-디코더 구조를 가지고 있다. 그러나 이전의 Seq2Seq모델과 다른 점은 인코더와 디코더라는 단위가 1개가 아닌 여러개가 존재할 수 있다는 점이다.

논문에서는 인코더를 6개 쌓았다고 하지만, 사용자가 얼마든지 변경할 수 있다. 디코더와 인코더의 개수 또한 자율적으로 쌓을 수 있다. 인코더들은 모두 같은 구조를 가지고 있지만, 그들 간에 Weight값을 공유하지 않고 있다. 이제부터 인코더로 들어가는 과정부터 차근차근 살펴보자.
2. 포지셔널 인코딩(Positional Encoding)
트랜스포머의 내부로 들어가기 전에 트랜스포머의 입력에 대해 먼저 알아보고자 한다. RNN이 자연어 처리에서 유용했던 이유는 단어의 위치에 따라서 순차적으로 입력받아서 처리했기 때문에 위치에 대한 정보를 받을 수 있었던 것이다.
그러나 Transformer는 단어 입력을 순차적으로 받는 방식이 아니므로 단어의 위치 정보를 다른 방식으로 알려주어야 하는데, 각 단어의 임베딩 벡터에 위치정보들을 더하여 모델의 입력으로 사용한다. 그것을 포지셔널 인코딩(Positional Encoding)이라 부른다.
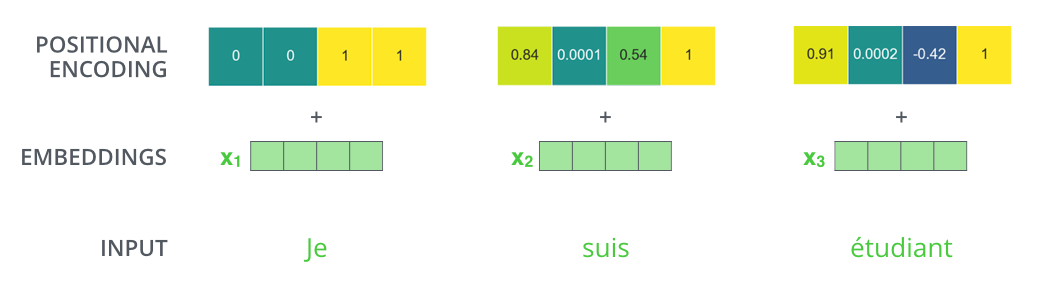
포지셔널 인코딩 값은 seq의 값들에 따라 영향을 받는 벡터가 아니다. 트렌스포머에서 위치정보를 반영하는 값인 Positional Encoding값의 정의는 아래와 같다.
$$ PE_{(pos, 2i)} = sin(pos/10000^{2i/d_{model}}) $$
$$ PE_{(pos, 2i+1)} = sin(pos/10000^{2i/d_{model}}) $$
각 위치에 사인 함수와 코사인 함수를 적용한 값인 포지셔널 인코딩 값을 임베딩 벡터에 더해줌으로 단어의 순서 정보를 더해주게 된다. 저 수식에서 말하는 pos와 $i, d_{model}$은 다음과 같이 정의한다.
- $pos$ : 입력 문장에서의 임베딩 벡터의 위치 (ex) je suis etudiant 에서 je)
- $i$ : 임베딩 벡터 내의 차원의 인덱스(트랜스포머에서는 각 인코더와 디코더의 임베딩차원이 동일하다)
- $d_{model}$ : 임베딩 벡터의 차원의 수
포지셔널 인코딩을 시각화 하면 다음과 같은데, 각 행은 문장에서의 단어 하나하나를 의미하고, 열은 단어를 임베딩 한 후의 벡터를 의미한다.

이 벡터들은 중간 부분이 반으로 나뉜 것 처럼 보이는데, 그 이유는 반쪽은 사인 함수에 의해 생성되고 나머지 반쪽은 코사인 함수에 의해 생성되었기 떄문이다. 이 두 값이 연결되어 하나의 포지셔널인코딩 벡터를 이루고 있다.
3. 어텐션(Attention)
트렌스포머에서 사용되는 세가지의 어탠션에 대해 간단히 이야기 하고자 한다.

첫번째 Encoder Self Attention, Masked Decoer Self Attention은 본질적으로 Query, Key, Value가 동일하다. Encoder, Decoer 어텐션은 Query가 디코더, Key, Value가 인코더 벡터이다.


위 세가지의 어텐션은 앞으로 인코더와 디코더에 들어가는데, 멀티헤드라는 이름이 붙은 이유는 트렌스포머가 어텐션을 병렬적으로 수행하기 때문이다.
4. 인코더(Encoder)
이제 인코더의 방식에 대해 알아보고자 한다. 하나의 인코더를 확대하면 아래와 같다.

인코더는 먼저 self Attention layer를 지나간다. 이 layer는 encoer가 하나의 단어를 encode하기 위해서 입력 내의 모든 단어들과의 관계를 살펴본다. self attention을 통과하고 나온 출력은 다시 feed-forward신경망으로 들어간다. 똑같은 feed-foward 신경망이 단어마다 독립적으로 적용되서 출력을 만든다.

조금 더 크게 들여다 본다면, 입력하는 문장에 대한 각 단어(토큰) 을 먼저 임베딩(논문에서는 512차원으로 임베딩)하고, 포지셔널 인코딩 벡터를 더해 나온 임베딩 벡터의 리스트를 셀프어텐션에 태운다. 그 다음으로 feed-forward 신경망에 통과시키고, 그 결과물을 다음 encoder에 전달한다. 그 사이에 Normalize하는 부분이 있지만, 그부분은 후에 설명하도록 하자.
5. Self-Attention
셀프 어텐션에 대한 개념부터 자세히 살펴보자. 어텐션 함수는 주어진 쿼리(Query)에 대해서 모든 키(Key)와 유사도를 각각 구한다. 그리고 구해낸 이 유사도를 가중치로 해서 키(Key)와 매핑된 값(Value)에 반영해준다 그리고 유사도가 반영된 값(Value)을 모두 가중합하여 리턴한다.
셀프 어텐션은 어텐션을 자기 자신에게 수행한다는 의미이다. Q, K, V를 입력 문장의 모든 단어 벡터들로 정의하는 것이다. 만일 우리가 "그 동물은 길을 건너지 않았다. 왜냐하면 그것은 너무 피곤하기 때문이다(The animal didn't cross the street because it was too tired)"라는 문장을 번역해야 한다고 생각해보자. 우리는 그것(it)이 동물(animal)인지, 길(street)인지 명확히 알 수 있지만 기계는 힘들어한다. 그러나 셀프 어텐션은 문장 내의 단어들끼리의 유사도를 구함으로서 그것(it)이 동물(animal)과 연관되었을 확률이 높다는 것을 찾는다.

5.1 Q, K, V 벡터 얻기
셀프 어텐션을 수행하기 위해 Q, K, V를 얻는데 이들의 차원은 임베딩한 벡터 512가 아니라 512에서 멀티 헤드로 병렬처리하는 만큼인 num_heads를 나눈 값을 차원으로 해서 얻는다. 논문에서는 num_heads를 8로 해서 Q, K, V의 차원은 512/8 = 64차원이 된다. Q, K, V를 생성하기 위한 가중치행렬 W가 존재한다.

5.2 스케일드 닷-프로덕트 어텐션(Scaled dot-product Attention)
self-attention의 두번째 연산은 Q와 K의 내적을 통해 attention score를 얻는다. 그리고 그리고 벡터 사이즈인 64의 제곱근인 8을 나눠주면 스케일드 닷 프로덕트 어텐션(scaled dot product attention)이 된다.

이렇게 나온 값을 softmax계산을 통해 모든 점수를 양수로 만들고 합이 1이 될 수 있도록 한다. 이 softmax 점수는 현재 위치의 단어의 encoding에 있어서 얼마나 각 단어들의 표현이 들어갈 것인지를 결정한다. 그리고 이 값들을 각 단어의 V값들에 곱해주며, 마지막으로 그 값을을 모두 더해준다.

이 모든 과정이 바로 self-attention의 계산 과정이다. 이과정으로 나온 결과를 feed forward 신경만ㅇ으로 보낸다. 그러나 하나하나의 단어를 연산하는 것이 아닌 행렬 연산을 통해 전체 문장의 값들을 계산한다
5.3 self attention 행렬연산
아까는 각 값들을 단어 하나하나씩 연산했다면 이제는 입력 단어 벡터들을 하나의 X로 쌓아올리고 가중치 행렬을 곱해 문장에 대한 Q, K, V를 구한다. 우리는 이 행렬의 self attention 단계를 하나의 식으로 압축할 수 있다.

위 식은 아래의 수식으로 나타낼 수 있다.
$$Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$$
위의 행렬 연산에 사용된 행렬의 크기를 정리하면, $QT(seq_len, 출력 임베딩 차원/멀티헤드 $d_v$)$K^T$($d_v$, seq_len) * $V$(seq_len, $d_v$)이므로 최종 (seq_len, $d_v$)의 크기를 갖게 된다.
6. 멀티 헤드 어텐션(Multi-head Attention)
앞서 설명한 Attention 값들은 출력 임베딩 차원에서 멀티헤드 개수에 대한 값을 나누었으므로 열의 길이가 줄어들었다. 멀티헤드의 의미는 이와 같은 self Attention을 병렬적으로 여러개 연산한다는 의미인데 아래와 같이 attention layer의 성능을 향상시킨다.
1. 모델이 다른 위치에 집중하는 능력을 확장시킨다.
2. attention layer가 여러개의 representation 공간을 갖게 해준다. 여러개의 query, key, value에 대한 weight행렬을 가지므로서 encoder, decoder마다 8개의 세트를 가지게 된다. 학습이 된 후 각각의 세트는 입력 벡터들이 곱해져서 벡터들을 각 목적에 맞게 투영시킨다.
멀티헤드어텐션을 통해 출력된 8개의 어텐션 값들을 열 기준으로 concatenate해준다.


이 모든 과정을 하나의 그림으로 표현을한 시작적 자료가 있다. (Jay Alammar 최고...)
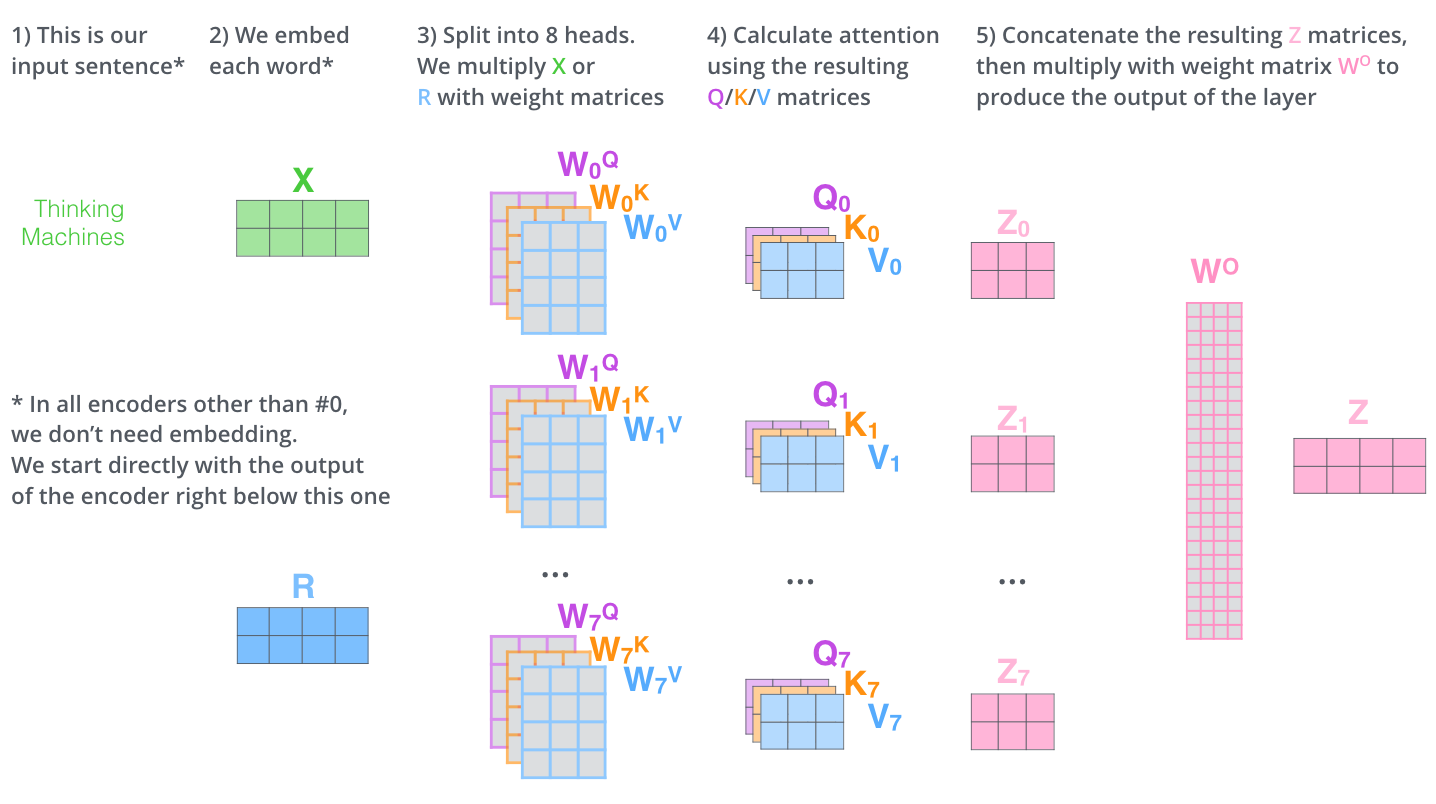
7. Add&Normalize (Residual connection, Layer Normalization)
self-attention을 통과하기 전에, Layer Normalize과정을 거치게 되는데, 이 과정을 시각화 하면 아래와 같다.

잔차 연결(Residual connection)은 서브층의 입력과 출력을 더하는 것을 말한다. 포지셔널 임베딩을 한 후의 값인 x와 멀티헤드 셀프 어텐션을 거치고 난 뒤의 값인 z를 더한다. 이를 수식으로 나타낸다면 $H(x) = x + Multi-head Attention(x)$와 같다.
그리고 층 정규화(Layer Normalization)을 거치는데, 잔차연결의 입력을 x, 라고 하고 정규화 연산을 거친 후의 결과를 LN이라고 한다면 수식은 다음과 같다. $LN = LayerNorm(x + Multi-headAttention(x)$ 층 정규화의 자세한 과정은 텐서의 마지막 차원에 대해 평균과 분산을 구하고, 이를 가지고 정규화하여 학습을 돕는다.

8. 포지션 와이즈 피드 포워드 신경망(Position wise FFNN)
마지막은 각 단어에 대한 어텐션 값을 Feed Forward를 각각 태워 출력시킨다. 이때 FFNN의 가중치행렬은 정방행렬로, 입력값의 차원과 출력값의 차원이 동일하다. 그래서 최종 출력은 여전히 인코더의 입력 크기였던 (seq_len, $d_model$)의 크기가 된다.
만일 우리가 2개의 인코더와 1개의 디코더 형태로 이루어진 형태의 transformer를 생각한다면 다음과 같은 모양이 될 것이다.

이렇게 인코더의 전 과정을 보게 되었는데, 디코더 과정은 다음 포스팅에 남길 계획이다.
아래는 이와 관련한 강필성교수님의 강의인데, 자연어 처리 강의에 유명하신 분이니 참고해서 들으면 좋을 듯 하다.
'AI Study > NLP' 카테고리의 다른 글
| [NLP/자연어처리] pre-trained model(1) - ELMo(Embeddings from Language Models) (0) | 2021.05.31 |
|---|---|
| [NLP/자연어처리] Seq2Seq4 - 트랜스포머(Transformer)_Decoder (0) | 2021.05.26 |
| [NLP/자연어처리] Seq2Seq(2) - 어텐션 매커니즘(Attention Mechanism) (0) | 2021.05.24 |
| [NLP/자연어처리] Seq2Seq(1) - RNN을 이용한 시퀀스 투 시퀀스 (0) | 2021.05.24 |
| [NLP/자연어처리] LSTM(Long Short-Term Memory), GRU(Gated Recurrent Unit) (0) | 2021.05.21 |