0. 들어가며
요즘은 단순 연구에서 뿐만이 아닌 실제 현업에서 설명가능한 AI, XAI를 많이 요구하고 있는 듯 하다. AI의 신뢰성과 결과의 이유가 궁금하기 때문인 것 같다. 또한 금융사에서도 AI 결과를 고객에게 설명하기 위해서도 XAI를 사용한다고 한다.
LIME이나 SHAP 등 XAI를 위한 활발한 연구가 이루어지고 있으며, 그에 대한 논문도 나오고 있지만 여전히 어려운 연구 과제 중 하나가 XAI라고 한다. 오늘은 어려운 이유와 함께 XAI에서 가지고 있는 문제점을 보완하기 위해 태어난 Integrated Gradient에 대해 설명해 보려고 한다.
1. 개요
0. 들어가며 에서도 말했지만 XAI를 위한, 그 중에서도 input feature가 모델의 output에 얼마나 영향을 끼쳤는지 나타내주는 값(attribution)을 파악하는데에 많은 연구와 방법론들이 나오고 있다. 그러나 여전히 그 연구가 쉽지 않은 이유는 정량적으로 XAI에 대해서 비교하고 성능을 평가하는 것은 쉽지 않기 때문이다. 일반적인 머신러닝 모델은 accuracy나 f1-score 등 많은 정량적인 판단 스코어가 있지만, attribution을 생성하는 모델의 경우는 정량적인 평가가 쉽지 않아 아직까지는 관계자의 만족도 정도로 성능을 평가하는 정도이다.
근데 이번 논문, ’Axiomatic Attribution for Deep Networks’에서는 이러한 문제의식을 바탕으로 연구가 진행되었다고 한다.
이번 논문에서는 attribution 방법론이 가져야 하는 주요한 성질(axioms)에 대해 설명하고, 그 성질을 만족한 Integrated Gradient 방법론에 대해서 제안한다.
2. Attribution을 파악한다는 것
Attribution을 파악한다는 것은 해당 모델에서 input과 output간의 관계를 파악하는 것이다. 다시 말해서, 학습된 모델이 예측을 할 때 input data의 한 feature가 예측된 output에 얼마나 큰 영향을 주었는지를 파악하는 것이다.
이번 논문에서는 attribution을 판단하는 방법을 위해 baseline이라는 의미가 없는 임의의 값(padding 값)을 두어 baseline과 input feature간의 차이를 비교하며 계산한다. 계산에 대한 수식과 정의는 아래와 같다.


여기서 a1, a2, an은 변수 중요도(feature importance)와 유사한 개념이다.
위에서 언급한 baseline에 대해서 조금 더 자세하게 설명하자면, 일종의 비교 대상이라고 할 수 있다. 좋은 baseline은 모델에 대해 중립적인 의미를 가지는 데이터 포인트라고 할 수 있다. 그래서 NLP에서는 pad 값, 이미지에서는 검은색이나 흰색의 zero pixel로 두어 사용하고는 한다.
3. Attribution을 파악하기 위한 두가지 Axioms
많은 attribution task의 문제 중 하나는 평가가 어렵다는 것이다. attribution이 높은 feature들을 제거해가면서 모델의 성능이 얼마나 떨어지는지를 파악하며 attribution을 파악하는 방법도 있다. 직관적으로는 상당히 좋지만, 일부 feature가 제거된 모델이 성능이 떨어진 이유가 feature가 중요해서인지, 모델이 학습하지 않은 분포의 데이터라 그런지는 명확한 설명이 어렵다는 단점이 있다.
이번 논문에서는 이런 한계를 극복하기 위해서 정량적인 평가보다, 주요한 성질(axioms)를 정의하고 이를 충족시키는 integradient 방법론을 제안한다. 두가지의 Axioms는 아래와 같다.
- Sensitivity
- Implementation Invariance
3-1. Sensitivity
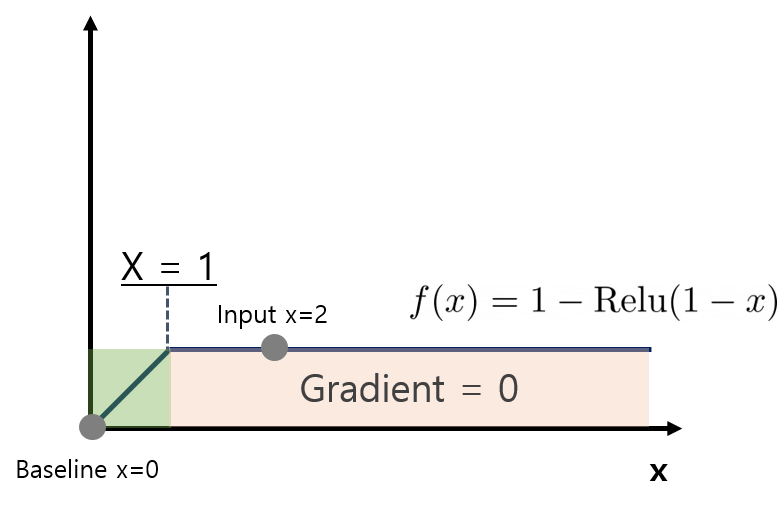
Sensitivity란 baseline과 input의 차이가 오직 하나의 feature이고 그 둘의 예측 결과가 다르다면, 차이나는 feature가 모델의 예측에 영향을 끼쳤다고 생각할 수 있다. 그리고 그 feature의 영향도가 0이 아니라면, Sensitivity 조건을 만족한다고 할 수 있다.
미리 말을 하자면 Gradients는 Sensitivity를 충족하지 못한다. 간단하게 모델 수식을 f(x) = 1-ReLU(1-x)라고 생각해보자. x가 0 일 경우 f(0)는 0이다. 하지만 x 가 2일 경우 f(2)는 1이다. Sensitivity 조건을 만족하기 위해서는 이 모델은 서로 다른 값을 넣었을 때, 다른 predict 값을 가져오기 때문에 gradients가 서로 달라야 한다. 그러나 그 둘의 Gradients는 동일하게 0이다.
3-2. Impementation Invariance
서로 다른 network이지만 같은 input ~output의 관계를 가진다면, 두 network는 동일한 attributon을 가져야 한다. 이러한 특성을 implementation invriance라고 한다.
Gradient는 Chain rule이 성립하기 때문에 Impementation Invariant하다는 장점을 가지고 있다. 그러나 LRP 혹은 DeepLIFP와 같은 attribution 방법론은 chain rule이 성립하지 않기 때문에 Impementation Invariant가 성립하지 않는다.

4. Integrated Gradient
Integrated Gradient는 이 둘의 조건을 만족시키기 위해서 제안된 방법론이다. Sensitivity에 대한 문제점은 극복하면서 Implementation invariance를 유지하는 방법이다.
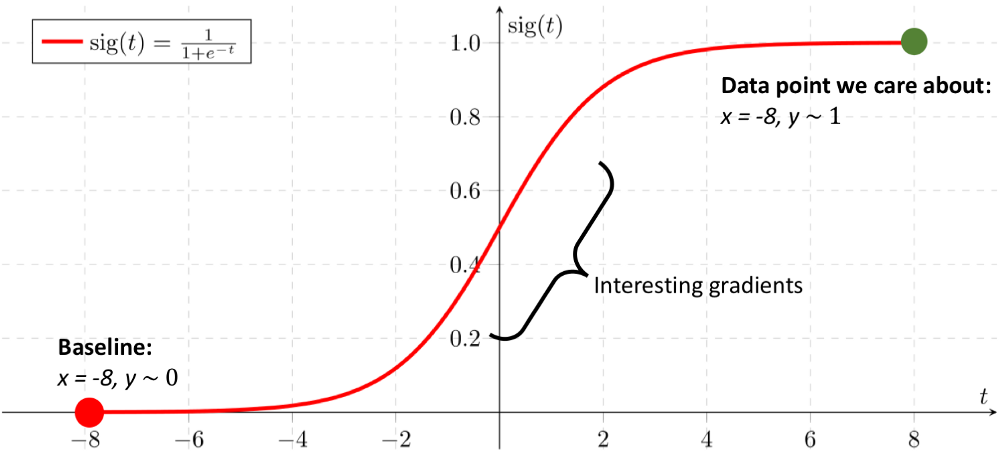
직관적으로 살펴본다면, Integrated Gradient는 baseline에서 input까지의 모든 gradient를 고려하는 방법이다. 특정 지점에서 Gradient값이 0 이 되는 이슈(Sensitivity)를 해결할 수 있으면서, gradient를 활용하므로 implementation invaricnce 하다.
Integrated Gradient를 구하는 수식은 아래와 같다.

5. Integrated Gradient 계산 방법
가볍게 설명하기 위해 Integrated Gradient 계산하는 순서에 대해 설명한다.
1단계 ) baseline( 픽셀 값이 모두 0인 이미지, pad값으로만 채워진 토큰 임베딩 백터, 자연수 0으로만 채워진 정형데이터 등) 에서 기준이 시작된다.
2단계 ) baseline과 원본 input feature과의 linear interpolation을 계산한다. 위 수식에서의 알파값을 0에서 시작하여 점점 늘려나가면서 값을 누적한다. 이미지의 경우 시각적으로 아주 어두운 이지에서 점점 밝아지는 효과를 볼 수 있다.

3단계 ) feature값이 하나 차이가 있는 baseline과 input feature의 차이를 Integrated Gradients로 계산한다.
4단계 ) 누적된 Gradients를 평균하여 attribution을 계산한다.
이에 데힌 로우한 코드는 아래 medium의 저자가 자세히 설명해주고 있다.
Understanding Deep Learning Models with Integrated Gradients
Understand and implement the Integrated Gradient technique to a variety of deep learning networks to explain the model's predictions.
towardsdatascience.com
6. 개인적으로 느낀 Integrated Gradient의 장단점.
이번 Integrated Gradient를 보고 직접 실험을 해보면서, 장단점을 생각해보았다.
첫번째 장점은, 어떤 모델에도 적용할 수 있다는 점이다. 결과 값을 가지고 연산을 하는 것이기 때문에, 이미지, 텍스트, 정형 데이터를 활용한 어떤 모델에서도 적용할 수 있다는 점이 큰 장점이다.
또한 LIME과 같이 별도 모델을 생성하지 않아도 되어서 모델에 대한 성능을 평가하지 않아도 된다는 점이 좋다. XAI 설명에 대한 성능 평가가 어려운 만큼, 모델 자체에 대한 성능은 간소화 하는게 제일 좋은 것 같다.
장점이 있는 만큼, 단점도 존재한다.
단점은, 알파의 개수를 정해주는 것에 따라 시간에 대한 차이가 좀 크게 발생한다는 점이다. 실시간으로 고객에게 설명을 해줘야 하는 경우, 알파 스텝이 크면 1건당 1초가 넘게 걸릴 수 있다.
또 하나는, 알파의 스텝을 결정할 수 있는 만큼, 학습모델은 아니지만, 스텝에 따라 성능이 바뀔 것 같다는 생각이 들었다. 사실 어떤게 더 좋은가에 대한 기준도 없기 때문에 조금 난해한 부분이 있다.
7. 마치며
제안된지 생각보다 오래된 논문이었고, 텍스트나 이미지 쪽에서는 이미 많이 사용되고 있는 방법론인 것 같다.
현업 프로젝트를 하려 할 때 해당 방법론을 쓰려 했으나, 예측 시간이 오래 걸린다는 이유로 현재 보류 중인 방법론이다.
앞으로 계속해서 XAI의 중요성이 대두될 것 같은데, 많은 연구가 나와 많이 적용해 볼 수 있었으면 좋겠다.
reference
https://rroundtable.github.io/blog/deeplearning/xai/2020/05/05/integrated-gradient.html
Integrated Gradient 정리글
Integrated Gradient 정리글
rroundtable.github.io
https://jjdeeplearning.tistory.com/17
Explainable AI - Integrated Gradients (IG)
Axiomatic Attribution for Deep Networks(Mukund Sundararajan et al.)에서 나온 개념이다. 일반적으로 우리가 사용하는 딥러닝 모델은 설명이 힘든 블랙박스 모델이다. 대부분의 딥러닝 모델은 온갖 비선형성을
jjdeeplearning.tistory.com
Understanding Deep Learning Models with Integrated Gradients
Understand and implement the Integrated Gradient technique to a variety of deep learning networks to explain the model's predictions.
towardsdatascience.com
'Study > etc' 카테고리의 다른 글
| [Trend] 대안 데이터(Alternative data)란? (1) | 2023.01.28 |
|---|---|
| [IT] NVIDIA 그래픽카드(GPU) 종류 간단정리 (0) | 2022.06.26 |
| [GCP]Computing Engine에 Python 분석 환경 구성하기(2) (0) | 2022.01.22 |
| [GCP] Computing Engine에 Python 분석 환경 구성하기(1) (0) | 2022.01.16 |
| [GCP] Google Cloud Platform Compute Engine VM 생성하기 (0) | 2021.12.19 |
![[XAI] Integrated Gradient 에 대하여](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbAZnqE%2FbtrWedWAvXK%2FTkmgb2SzeK3wvM4vBmBaGK%2Fimg.png)