반응형
Deeper Look at Gradient Descent
- Hypothesis function
- Cost function 이해
- Gradient descent 이론
- Gradient descent 구현
- Gradient descent 구현(nn.optiom)
Hypothesis (Linear Regression)
Hypothesis function은 인공신경망의 구조를 나타내는데 주어진 input에 대해 어떤 output을 나타내는지 𝐻(𝑥)H(x)로 표현한다.
$${H(x) = Wx + b}$$
- ${W}$ : Weight
- ${b}$ : bias

What is the best model?
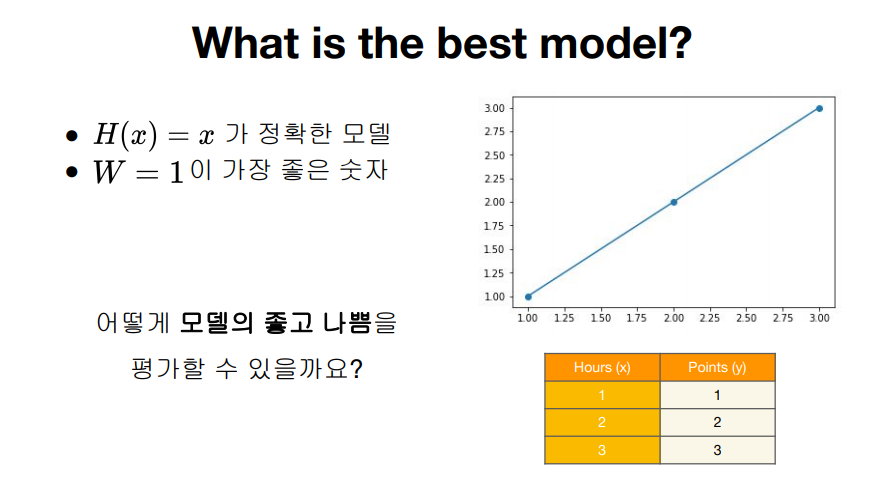
Cost function
- 모델 예측값이 실제 데이터와 얼마나 다른지 나타내는 값
- 잘 학습된 모델일수록 낮은 cost를 가진다.

- W = 1일 떄 cost = 0
- 1에서 멀어질수록 cost는 커진다.


미분
- ${cost(W) = \frac{1}{m}\sum_{i=1}^{m}(Wx^{(i)} - y^{(i)})^2}$
- ${\nabla{W} = \frac{\partial{cost}}{\partial{W}} = \frac{2}{m}\sum_{i=1}^{m}(Wx^{(i)} - y^{(i)})x^{(i)}}$
- ${W : = W - \alpha \nabla{W}}$
실습코드
## full code
## data
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
## model 초기화
W = torch.zeros(1)
# learning rate
lr = 0.1
## epoch : 데이터로 학습한 횟수
## 학습하면서 점점 1에 수렴하는 w와 줄어드는 cost를 알 수 있음
nb_epochs = 10
for epoch in range(nb_epochs + 1):
# b = torch.zeros(1, requires_grad = True)
hypothesis = x_train*W
# cost gradient 계산
cost = torch.mean((hypothesis - y_train)**2)
gradient = torch.sum((W*x_train - y_train) * x_train)
print('Epoch {:4d}/{} W: {:3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), cost.item()
))
W -= lr*gradient
>>>
Epoch 0/10 W: 0.000000 Cost: 4.666667
Epoch 1/10 W: 1.400000 Cost: 0.746666
Epoch 2/10 W: 0.840000 Cost: 0.119467
Epoch 3/10 W: 1.064000 Cost: 0.019115
Epoch 4/10 W: 0.974400 Cost: 0.003058
Epoch 5/10 W: 1.010240 Cost: 0.000489
Epoch 6/10 W: 0.995904 Cost: 0.000078
Epoch 7/10 W: 1.001638 Cost: 0.000013
Epoch 8/10 W: 0.999345 Cost: 0.000002
Epoch 9/10 W: 1.000262 Cost: 0.000000
Epoch 10/10 W: 0.999895 Cost: 0.000000Gradient Descent with torch.optim
- torch.optim으로도 gradient descent를 할 수 있다.
- 시작할 때 optimizer를 정의
- optimizer.zero_grad()로 gradient를 0으로 초기화
- cost.backward()로 gradient 계산
- optimizer.step()으로 gradient descent
# optimizer 설정
optimizer = torch.optim.SGD([W], lr = 0.15)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()실습
## full code
## data
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
## model 초기화
W = torch.zeros(1, requires_grad = True)
# optimizer 설정
optimizer = torch.optim.SGD([W], lr = 0.15)
## epoch : 데이터로 학습한 횟수
## 학습하면서 점점 1에 수렴하는 w와 줄어드는 cost를 알 수 있음
nb_epochs = 10
for epoch in range(nb_epochs + 1):
# b = torch.zeros(1, requires_grad = True)
hypothesis = x_train*W
# cost gradient 계산
cost = torch.mean((hypothesis - y_train)**2)
print('Epoch {:4d}/{} W: {:3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), cost.item()
))
# cost로 H(x) 개선
optimizer.zero_grad() # gradient 0으로 초기화
cost.backward() ## gradient 계산
optimizer.step() ## gradient descent
>>>
Epoch 0/10 W: 0.000000 Cost: 4.666667
Epoch 1/10 W: 1.400000 Cost: 0.746667
Epoch 2/10 W: 0.840000 Cost: 0.119467
Epoch 3/10 W: 1.064000 Cost: 0.019115
Epoch 4/10 W: 0.974400 Cost: 0.003058
Epoch 5/10 W: 1.010240 Cost: 0.000489
Epoch 6/10 W: 0.995904 Cost: 0.000078
Epoch 7/10 W: 1.001638 Cost: 0.000013
Epoch 8/10 W: 0.999345 Cost: 0.000002
Epoch 9/10 W: 1.000262 Cost: 0.000000
Epoch 10/10 W: 0.999895 Cost: 0.000000
출처 : www.boostcourse.org/ai214/lecture/42285
파이토치로 시작하는 딥러닝 기초
부스트코스 무료 강의
www.boostcourse.org
반응형
'Study > DL_Basic' 카테고리의 다른 글
| [파이토치로 시작하는 딥러닝 기초]05_ Logistic Regression (0) | 2020.12.22 |
|---|---|
| [파이토치로 시작하는 딥러닝 기초]04.02_Loading Data (0) | 2020.12.21 |
| [파이토치로 시작하는 딥러닝 기초]04.01_Multivariable_Linear_regression (0) | 2020.12.21 |
| [파이토치로 시작하는 딥러닝 기초]02_Linear Regression (0) | 2020.12.21 |
| [파이토치로 시작하는 딥러닝 기초]01_Tensor Manipulation(텐서 조작) (0) | 2020.11.26 |
![[파이토치로 시작하는 딥러닝 기초]03_Deeper Look at Gradient Descent](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FyPRqh%2FbtqQ1Noj7fP%2FiSYiJdOrS8SfuwV7Jl8Ms0%2Fimg.png)